[문제 풀이]행성 터널(백준_2887)
Updated:
백준 문제 2887, 행성 터널 풀이
행성 터널 문제를 풀다가 답을 맞기는 했는데 왜 이 답이 나오는 줄은 아는데 이 답의 풀이 과정이 정확히 이해가 안될 때가 있다. 이 문제가 그러했다. 처음에 문제 설명란의 “A 행성과 B 행성 사이의 간선 비용은 min( |Xa - Xb|, |Ya-Yb|, |Za-Zb| ) 이다.” 라는 부분을 보고 어렵지 않다고 생각하고 이부분에 대한 함수를 작성하였다. 각 정점에서 다른 정점들로 가는 x축, y축 그리고 z축으로 가는 비용중 최소 비용을 가진 축의 간선 비용을 구하면 된다고 생각했다. 맞는 말이지만 구현방법을 곧이 곧대로 밀고 나간게 문제였다.
// min( |Xa - Xb|, |Ya-Yb|, |Za-Zb| ), 행성 a 와 b의 x축 y축 z축의 거리중에서 가장 짧은 거리를 최소 비용으로 반환
int getMinDistance(pair<int, pair<int, int> > a, pair<int, pair<int, int> > b){
int Xa = a.first;
int Xb = b.first;
int Ya = a.second.first;
int Yb = b.second.first;
int Za = a.second.second;
int Zb = b.second.second;
return min(Xa - Xb, min(Ya - Yb, Za - Zb));
}
vetor<pair<int, pair<int, int> > > graph;
vector<int> minDistances;
for(int a = 0; a < graph.size(); a++){
for(int b = a + 1; b < graph.size(); b++){
int minDistance = getMinDistance(graph[a], graph[b]);
minDistances.push_back(minDistance);
}
}
하지만 이렇게 되면 메모리 초과 판정을 받는다. 두 행성 A(Xa, Ya, Za) 와 B(Xa, Ya, Za)를 터널로 연결할 때 드는 비용이 min( |Xa - Xb|, |Ya-Yb|, |Za-Zb| ) 라고 할때, 각 행성에서 다른 모든 행성으로 가는 간선 비용을 각각 구한다고 해보자. A 행성에서 다른 행성을 구한다고 하면 N(N - 1) 의 공간 복잡도가 발생한다. 이는 행성 갯수가 최대 100,000 개 임을 감안하면 100,000 * 99,999 의 메모리가 소요 되는 것이다. 125MB 메모리 제한이 있기 때문에 메모리 초과로 인해 오답 판정을 받는다. 그렇다면 어떻게 하면 될까. 힌트는 min( |Xa - Xb|, |Ya-Yb|, |Za-Zb| ) 조건에 있다. 각 정점의 위치 좌표들인 X, Y, Z 를 좌표별로 오름차순으로 정렬시킨후, 순서대로 간선을 이어주고 비용을 계산하자. 그리고 이 간선들에 대한 정보를 전부 저장 후, 간선들의 비용을 오름차순 정렬 후 크루스칼 알고리즘을 수행하면 된다.
예를 들어서 A, B, C, D 의 행성이 있을때 x 좌표별로 오름차순 정렬을 했을때 B-C-D-A 가 되었다고 하자. 그러면 B-C, C-D, D-A 로 순으로 연결되는데 x 좌표 기준으로 B(혹은 C)는 C(혹은 B)와 연결되었을때, C(혹은 D)는 D(혹은 C)와 연결되었을 때, D(혹은 A)는 A(혹은 D)와 연결되었을 때가 가장 최소 간선 비용을 가진다. 즉 이렇게 연결되야만 최소 x 좌표 기준으로 최소 간선 비용을 가진다. 이런식으로 y좌표 z좌표도 진행해주고 이들을 크루스칼 알고리즘으로 해결하면 된다. 그림으로 한번 풀어보면 다음과 같다
1번 행성: (x:11, y:-15, z:-15)
2번 행성: (x:14, y:-5, z:-15)
3번 행성: (x:-1, y:-1, z:-5)
4번 행성: (x:10, y:-4, z:-1)
5번 행성: (x:19, y:-4, z:19)
x축 중심의 총 최소 간선 비용을 가지는 그래프의 각 간선들, y축 중심의 총 최소 간선 비용을 가지는 그래프의 각 간선들, 그리고 z축 중심의 총 최소 간선 비용을 가지는 그래프의 각 간선들을 구한다.

그리고 이 모든 축들의 각 간선들을 가지고 또 최소 간선 비용을 가지는 그래프를 만드는 것이 핵심이다. 즉, 최소 비용을 가지는 위의 세 축의 그래프들에서 최소 간선 비용을 가지는 간선들을 차례대로 골라보면 아래와 같다. 참고로 같은 간선 비용을 가지면서 사이클을 가지는 경우는 x, y, z 순으로 선택이 된다.

그리고 완성된 최소 간선 그래프는 아래와 같다.
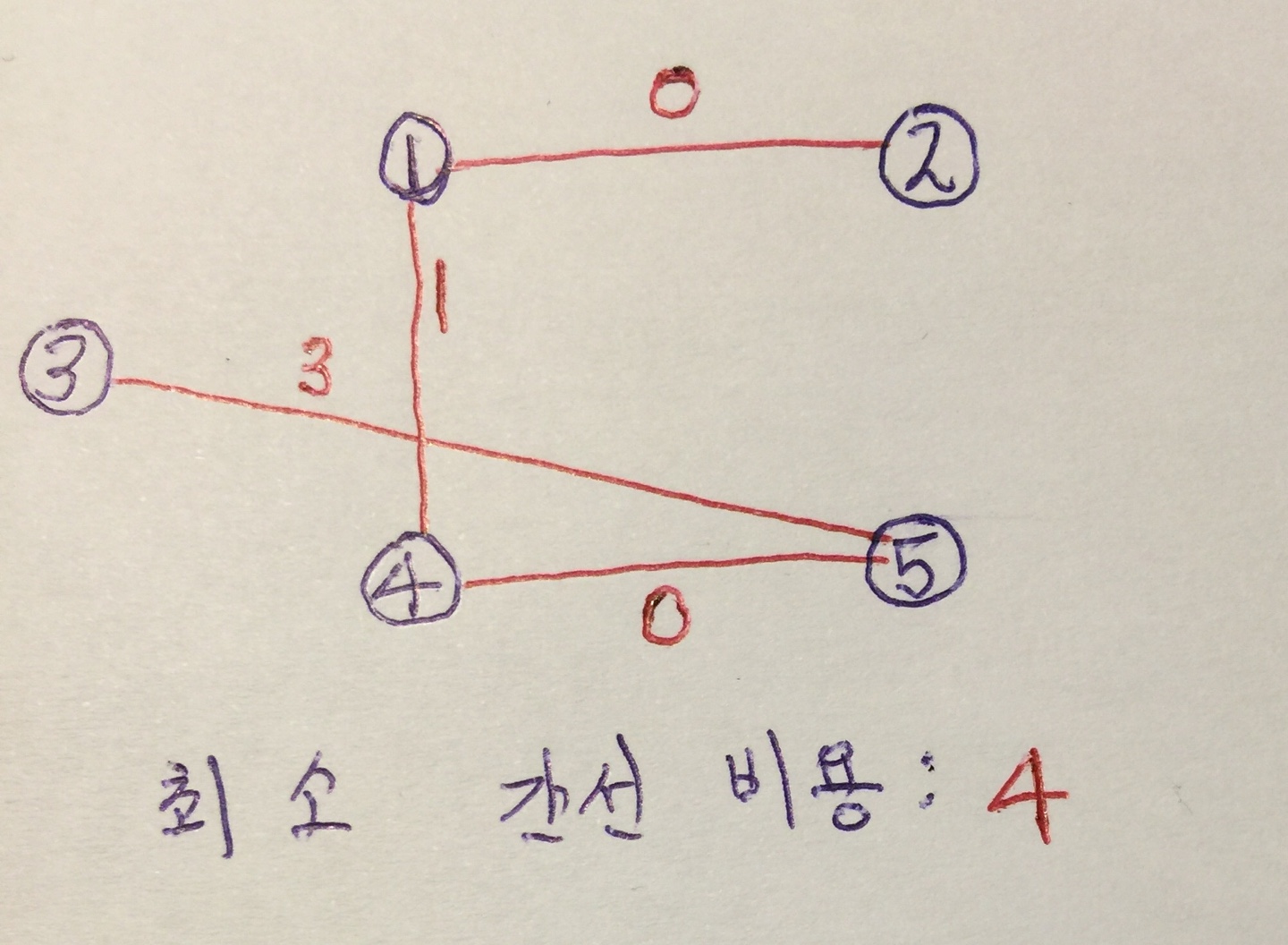
최종 소스 코드는 아래와 같다.
#include <iostream>
#include <algorithm>
#include <vector>
#include <utility>
using namespace std;
//problem link: https://www.acmicpc.net/problem/2887
int n;
vector<pair<int, pair<int, int> > > graph;
int parent[100001];
bool compare(pair<int, pair<int, int> > a, pair<int, pair<int, int> > b){
return a.second.second < b.second.second;
}
int findParent(int x){
if(parent[x] == x){
return x;
}
else{
return parent[x] = findParent(parent[x]);
}
}
void unionParent(int a, int b){
int parent_a = findParent(a);
int parent_b = findParent(b);
if(parent_a < parent_b){
parent[parent_b] = parent_a;
}
else{
parent[parent_a] = parent_b;
}
}
int main(void){
vector<pair<int, int> > sorted_x, sorted_y, sorted_z;
cin >> n;
for(int i = 0; i < n; i++){
int x, y, z;
cin >> x >> y >> z;
sorted_x.push_back(make_pair(x, i)); // x 좌표
sorted_y.push_back(make_pair(y, i)); // y 좌표
sorted_z.push_back(make_pair(z, i)); // z 좌표
}
sort(sorted_x.begin(), sorted_x.end()); // x 좌표 오름차순 정렬
sort(sorted_y.begin(), sorted_y.end()); // y 좌표 오름차순 정렬
sort(sorted_z.begin(), sorted_z.end()); // z 좌표 오름차순 정렬
for(int i = 0; i < n - 1; i++){ // n 개의 정점이 모두 연결된 최소한의 간선 갯수는? n-1 개다
// 순서대로 연결된 A행성과 B행성의 각 좌표별 최소 간선 비용을 구하자
int offset_x = sorted_x[i + 1].first - sorted_x[i].first;
int offset_y = sorted_y[i + 1].first - sorted_y[i].first;
int offset_z = sorted_z[i + 1].first - sorted_z[i].first;
// 그리고 연결된 A행성과 B행성의 번호들과 그 간선 비용들을 모두 넣어주자
graph.push_back(make_pair(sorted_x[i].second, make_pair(sorted_x[i + 1].second, offset_x)));
graph.push_back(make_pair(sorted_y[i].second, make_pair(sorted_y[i + 1].second, offset_y)));
graph.push_back(make_pair(sorted_z[i].second, make_pair(sorted_z[i + 1].second, offset_z)));
}
// 최소 간선 비용을 구하기 위해 오름차순 정렬을 하자
sort(graph.begin(), graph.end(), compare);
for(int i = 0; i < n; i++){ // 0번 행성 ~ n - 1 번 행성
parent[i] = i; // 자기 자신에 속하게 함
}
// x축 중심의 총 최소 간선 비용을 가지는 그래프의 각 간선들
// y축 중심의 총 최소 간선 비용을 가지는 그래프의 각 간선들
// z축 중심의 총 최소 간선 비용을 가지는 그래프의 각 간선들
// 이 모든 축들의 각 간선들을 가지고 또 최소 간선 비용을 가지는 그래프를 만드는 것이 핵심이다.
int result = 0;
for(int i = 0; i < graph.size(); i++){
int a = graph[i].first; // a 행성과
int b = graph[i].second.first; //b 행성이
int cost = graph[i].second.second; //연결된 간선의 비용
if(findParent(a) != findParent(b)){ // 같은 그룹에 속해있지 않다면(사이클이 생성된게 아니라면)
unionParent(a, b); // 같은 그룹으로 속하게 하고
result += cost; // 그 비용을 구해 최소 간선 비용을 구한다
}
}
cout<<result<<'\n';
}


Leave a comment